One of the most versatile techniques to model a data set using a formula is a formula to ensure it is the ratio of two polynomials:
. A rational formula is basically a non-linear formula. In order to model a dataset to a rational way, the strategy is to "remove" the rational, multiplying both sides of the formula being used as a model for the denominator Q (X) 
, which we have a relation of the form:
, which we have a relation of the form: Y (X) ∙ Q (X) = P (X)
then remove the brackets from the left side of this relationship by multiplying all terms of Y (X) 
by all the terms of Q (X)
after which cleared the left to leave the variable
And 
by all the terms of Q (X) after which cleared the left to leave the variable
one on that side with the remaining right side. Once we have taken this out, we just the way formula required to apply the matrix method, thereby avoiding the painful task of having to be deriving the normal equations corresponding to each particular model you want to use. A very important thing to always bear in mind when carrying out a modeling using a rational way is to look for the presence of roots in the
polynomial Q (X)
that may be within the range of data being modeled because such roots make the polynomial Q (X) take a value of zero, consequently resulting in a division by zero which
value Y (X)
just takes an undefined value in that (s) point (s). The presence a division by zero may be reason enough to dismiss some replacing it with a rational model.
The general expression for the rational formula used to model experimental data is as follows:
Here X is the dependent variable, Y is the independent variable, and A
1, A 2
, A 3 , etc. are the coefficients to be determined, which assume linear .
Although the rational function is non-linear, and apparently beyond the scope of the method of least squares, this function can be linearized clearing the denominator on the right side and put it as:
Y (1 + A 2
X + A X 
4
2 
4 + A 6 X 3 + ...) = A 1
3
+ A X + A
5
X ² + ... This can be rearranged as follows: Y = A 1 - A 2 XY + A 3 X - A 4 X 2 Y + A 5 X
2 - A
6 X 3 Y + ... Some of the terms on the right side containing both the dependent variable Y as the independent variable X, which apparently would be a problem. However, it is not, because in carrying out setting data to the formula both X and Y are known vectors of numerical values, the same data that is going to get the formula and what we care to accounts are the coefficients A 1, A 2, A 3 , etc. we are looking for, and how all these coefficients are linear, we can identify them even with the matrix method we have studied. may sound simple formula of all is the following: And it is on this formula and will hold the following resolution
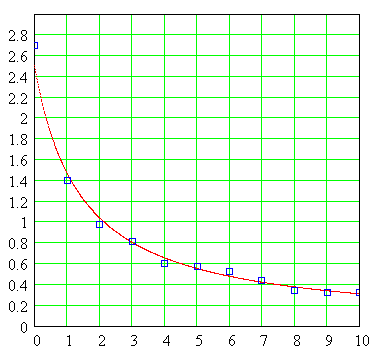
PROBLEM: Set the following data set
___ (
0 X, Y 
0
) = (0,2.7) ____ 
0
(
1 X, Y
1) = (1,1.4) _ __ (2 X, Y 2) = (2,0.98) _ __ (3 X, Y 3) = (3,0.82) ___ ( X 4 , Y 4 )=(4,0.61) ___ ( X 5 , Y
5
)=(5,0.58) ___ ( X 6 , Y 6 )=(6,0.53) __ _ ( X 7 , Y 7 )=(7,0.44) ___ ( X 8 , Y 8 )=(8,0.35) ___ ( X 9 , Y
9
)=(9,0.33) ___ ( X 10 , Y 10 ) = (10,0.33) a rational way type Y (X) = A / (1 + BX) . Multiplying both sides of the formula we have 1 + BX: Y (1 + BX) = A Clearing to put everything in terms of And :
Y = A - bxy Drawing on matrix method, we build first a vector
And
with the data for Y:
Y = [2.7 1.4
_ _ _ .98 .82 _
.
61 .58 _ _ _
.53 .44 .35
_ _ _
.33 .33] then build the data matrix X consisting of 11 rows and ten columns, based in the last formula we have above. The first column contains only "some" (1), which corresponds to the parameter values \u200b\u200b X raised to the zero power. The second column is formed by the negative output of the respective values \u200b\u200bof X and Y : now obtain the coefficient matrix K
: K = X T X ∙
The constant vector is:
V = Y ∙ X V = [9.7 -15,158
_] 
Finally, the solution is given by: S = K -1
T ∙ V
value that appears in the first row is
A
= 2,506, while the value appearing in the second line is B = 0,698. Then the formula we are looking for is:
The graph of this formula superimposed on the discrete data that is generated as follows:
As we can see, the data fit the rational formula is reasonably good. We can assume that the reason why data will not fall exactly along the curve is due to experimental error inherent in the data for reasons that are beyond the control of the experimenter.
PROBLEM: Given the following data: 
represent these data with rational functions of "least-squares fit" using the following ratios of two polynomials: (1)
(2)
(1) Although this rational function is a non-linear, we linearized by multiplying both sides of the equation by the denominator polynomial:
Y (1 + A 2
X) = A 1 
After that, cleared to leave the variable and one on the left side: 
Y = A
XY Since the coefficients A and A
1 2
we are looking for are linear (constant number), there is no problem in extending the matrix method of "least-squares fit" for the coefficients. We are first a vector Y with the values \u200b\u200bof Y:
then form the data matrix X, carefully noting that each column corresponds to what we put into the equation clear of Y. Since there are four pairs of experimental data, we know that this will be a matrix four lines, and will be a two column matrix corresponding to the terms that appear on the right side of the equation clear for Y. As in previous cases we have studied the application of the matrix, the first column of the matrix consists of four lines with "some." The second column of this array of data, according to what we have in the second term of the equation clear of Y, should be formed by the negative of the respective products of the values \u200b\u200bof X and Y:
This done, apply the abbreviated formula for the solution matrix of coefficients that are looking for:
S = (X
∙ T X) -1 ∙ (X
T ∙ Y) with which we obtain the coefficients
A
1 = 0.586561 and A 2 =- 0.989717. Since the values \u200b\u200bof the coefficients determined numerically, the least-squares rational formula is: Then there is the curve graph modeled by the least squares rational function with the original discrete data superimposed on the same graph:
is instructive to compare the numerical values \u200b\u200bpredicted by the formula obtained with the original discrete data:
Y (75) = 2.27
Y (9) = 5368 
Y (. 95) = 9.81
Y (99) = 6.29
Y (. 95) = 9.81 Y (99) = 6.29
We see that in the four cases are difficult to detect small differences in the graph.
(2) Now do the modeling with the formula that increases a term of X ² in the denominator of the rational function. 
Again, although this rational function is a nonlinear function can also linearized by multiplying both sides of the equation by the denominator polynomial:
Y (1 + A 
Again, although this rational function is a nonlinear function can also linearized by multiplying both sides of the equation by the denominator polynomial: 2
X + A
2
X ²) = A
1
After that, cleared to leave the variable and one on the side left:
Y = A 1
After that, cleared to leave the variable and one on the side left:
1
- A
2
XY - A
3
X ² Y
Since the coefficients A 1 , A 2 and A 3
we are looking for are linear ( numerical constants), there is no problem in extending the matrix method of "least-squares fit" for these coefficients. The vector of values \u200b\u200band remains the same, there will be no change there. What will change is the data matrix, which we carefully observing each column corresponds to what we put into the equation clear of Y. There remain four pairs of experimental data with which the data matrix remains four lines, but now is an array of three columns correspond to terms that appear on the right side of the equation clear for Y. As in previous cases we have studied the application of the matrix, the first column of the matrix consists of four lines with "some." The second column of this array of data, according to what we have in the second term of the equation clear of Y, must be formed by the negative of the respective products of the values \u200b\u200bof X and Y. And the third column of the data matrix, according to what we have in the third term of the equation clear of Y, must be formed with the negative output of the square of the values \u200b\u200bof X and Y values \u200b\u200bfor The data matrix X that we find is:
we are looking for are linear ( numerical constants), there is no problem in extending the matrix method of "least-squares fit" for these coefficients. The vector of values \u200b\u200band remains the same, there will be no change there. What will change is the data matrix, which we carefully observing each column corresponds to what we put into the equation clear of Y. There remain four pairs of experimental data with which the data matrix remains four lines, but now is an array of three columns correspond to terms that appear on the right side of the equation clear for Y. As in previous cases we have studied the application of the matrix, the first column of the matrix consists of four lines with "some." The second column of this array of data, according to what we have in the second term of the equation clear of Y, must be formed by the negative of the respective products of the values \u200b\u200bof X and Y. And the third column of the data matrix, according to what we have in the third term of the equation clear of Y, must be formed with the negative output of the square of the values \u200b\u200bof X and Y values \u200b\u200bfor The data matrix X that we find is:
With this, we have everything we need to apply again the general shorthand for the solution matrix of coefficients that are looking for:
S = (X ∙ T X) -1 ∙
(X
T ∙ Y) After following this matrix calculation, we obtain the coefficients
A
1 = 0.826773, A 2 =- 0.493931 and A 3 =- 0.492576. With the values \u200b\u200bof the coefficients determined numerically, the least-squares rational way that we find is:
Then there is the curve graph modeled by the rational function least squares with data original discrete superimposed on the same graph:: values \u200b\u200bpredicted by the formula obtained with the original discrete data are:
Y (75) = 2.34
Y (9) = 5.26 
Y (95) = 9.53
Y (99) = 7.28
Y (95) = 9.53 Y (99) = 7.28
these data represent a rational function of "least-squares fit" using the following ratio of two polynomials:
Multiplying both members of the equation by the denominator polynomial gives:
Y (1 + A 2 
X + A 4
X ²) = A
1 
X + A 4 X ²) = A
+ A 3 X
Solving for the variable Y alone: \u200b\u200b 
Y = A
1
- A 
Y = A 1
2
XY + A
3
X - A 4 X ² Y Since the coefficients A 1 , A 2
, A
3 , A
and A
4
we are looking for linear, nor is there here any problem in extending the matrix method of "least-squares fit" for the coefficients.
We are first a vector Y with values Y:
then form the data matrix X, carefully noting that each column corresponds to what we put into the equation clear of Y. Since there are ten pairs of experimental data, we know that this will be an array of ten lines, and will be an array of four columns correspond to terms that appear on the right side of the equation clear for Y. As in previous cases we have studied the application of the matrix, the first column of the array consists of ten lines with "some." The second column of this array of data, according to what we have in the second of the equation clear of Y, should be formed by the negative of the respective products of the values \u200b\u200bof X and Y:
The third column of the array of data to be carried in the third column X values, according to what we have in the third term of the equation clear of Y.
Finally, the fourth column, according to the fourth term in the equation we clear of and must be formed with the negative of the respective products of the square of the values \u200b\u200bof X and Y values
This done, apply the abbreviated formula for the solution matrix with coefficients we are seeking: 
S = (X
∙ T X) -1
S = (X ∙ T X) -1
∙ (X
T
∙ Y)
Whereupon we get: with the values \u200b\u200balready certain numerical coefficients, the least-squares rational formula is:
Then there is the curve graph modeled by the least squares rational function:
As can be seen, the curve fit to the data is excellent, almost ideal.
The chart illustrates another type of situations in which a rational function is used to perform modeling, those in which the data is not decline following a straight line but a curve.
PROBLEM: Given the following data: 
also make a graph of the resulting curve. What lessons can we learn from this exercise? 
Proceeding as we did in all the above problems, we find that the least squares formula for the rational function is given as follows:
Proceeding as we did in all the above problems, we find that the least squares formula for the rational function is given as follows:
Y (9) = 5.39
Y (95) = 9.28 Y (99) = 29.46
Accordingly
, of the data we have is almost perfect, all four discrete points fall directly along the curve.
Without
However, by plotting the obtained rational function, find the following: 
Our model exhibits a severe discontinuity, and in fact we have two different curves. If we make a statistical test of correlation between the original discrete data and the results predicted by the rational formula in the vicinity of such points, mathematically speaking, the fit is almost perfect. However, the presence of discontinuity, which can not be inferred from a near-perfect fit indicated by the correlation index, we stressed the great importance of an early graph of any formula that is modeling a dataset, because we can bring nasty surprises like this that can force us to completely discard certain pattern. It is not difficult to see the origin of the discontinuity, since the quadratic polynomial used in the denominator has two roots, one of which falls precisely within the range of values \u200b\u200bthat is being modeled, and taking X the value of this result we has experienced the sudden jump in the graph that point.
If we review the discrete data we are modeling, we see that these data are the same as used in the second problem of this section, where we use other models whose graphs did not show the problem we have here, this although we add an additional term in the numerator (A
3
X) could perhaps haben given a more precise curve yet. But this search for additional precision backfired because instead of having a bend better what we achieved was a curve with a serious problem that had no previous curves. This highlights another important point: we must be cautious in trying to obtain a model more and more complex, because in many cases, as we have seen here, greater complexity does not guarantee a better outcome.
If we review the discrete data we are modeling, we see that these data are the same as used in the second problem of this section, where we use other models whose graphs did not show the problem we have here, this although we add an additional term in the numerator (A
3
X) could perhaps haben given a more precise curve yet. But this search for additional precision backfired because instead of having a bend better what we achieved was a curve with a serious problem that had no previous curves. This highlights another important point: we must be cautious in trying to obtain a model more and more complex, because in many cases, as we have seen here, greater complexity does not guarantee a better outcome.
0 comments:
Post a Comment