3: The least-squares parabola
data adjustment formula using a linear model is excellent when the data follow a linear trend. However, in many cases the data does not follow a linear trend. Consider as an example the following ten data collection:
Friday, March 28, 2008
If we plot this collection of ten data points, we get the following: 
From the graph it is unclear how we can describe this Library data with a linear empirical formula. We
force a straight line on this data collection carried out regression analysis, by blindly usual mathematical calculations to obtain the "best fit" linear. However, the formula thus obtained we may not be very useful to estimate what will happen with other values \u200b\u200bare not plotted.
If we get the idea that this data collection can be best described by a non-linear model bx + cx 2 + dx
3
+ ex
. This certainly would go exactly curve for each points of the graph, as shown below:
What is the empirical formula can best fit these data? Try
perform a least-squares fit to obtain the regression line that best approximates the three data shown in the graph will una pérdida de tiempo, ya que los puntos no muestran tendencia alguna de agruparse en las proximidades de una línea recta. Sin embargo, podemos tratar de llevar a cabo aquí un ajuste utilizando como modelo un polinomio cuadrático, haciendo pasar los tres puntos
exactamente
a lo largo del polinomio:
P(X) = a 0 + a
1
X + a
Sustituyendo los tres pares de datos
A
( X
1
,
2 )=(2,8) and C ( X 2 , And 2) = (3,2) in the quadratic polynomial: 1 = a 0 + a 1 (1) + a 2 (1) 2 8 = a 0 + a 1 (2) + a 2 (2) 2
0
+
1
is that if you subsequently collect additional data values And at other points of X such as X = 1.5 and X = 2.5, such additional points can not be used to refine the model, since its derivation does not support more than three pairs, in which case the gathering of additional data only serve to confirm or reject the quadratic formula obtained, not to improve and refine it.
PROBLEM: Carry out an exact fit
of the following
X
1
= -1, 1 And = 0
X 2 = 0, And
2 = 0
there much data as i coefficients in the polynomial, which allows us to perform accurate adjustment
otherwise could not be carried out if there were fewer data or more data coefficients coefficients. To perform accurate adjustment
3 to 0 + a 1
(0) + a 2
cubic polynomial representing the four pairs of data is then:
All the points fall exactly on the curve
as we had anticipated.
X =- 0.5, and X
= +1.5 X where the values \u200b\u200bof P (X) amount sharply. For polynomials of high degree, this oscillatory behavior can turn violent in a matter completely unpredictable, to be a direct consequence of insisting on carrying out an exact modeling then go all the experimental data on a curve.
The interpolation procedure is appropriate to solve problems analytically accurate, which does not happen with the experimental data where the data rarely "fall" just a value that could be considered ideal, where the dispersion of data with respect to a set "ideal" is due to experimental error and where it is meaningless to try to fit exactly a certain amount of data to a polynomial formula. That is why, as well as fitting a linear formula to a collection of data that seem to follow a linear trend to use the method of least squares, the same method of least squares is extended to formulas can be applied to polynomial, allowing us to maintain the degree of the polynomial under control without allowing it to grow disproportionately to be adding additional pairs of points (in other words, under the criterion of least squares we try to fit 101 pairs of points a quadratic polynomial or a cubic polynomial instead of being forced to have recourse to a polynomial of degree 100 if you insist on trying to carry out an exact adjustment data to the formula that we are developing). If a set of data pairs to be plotted does not show a clustering around a straight line but around a curve, as a first approximation we can try to make an "adjustment" to the basic curve of all, the parable
, which in simple terms means attempting to carry out the data fit a quadratic polynomial as follows: Y = a + 0 to 1 X + a
2 X ²
has done a slight change of notation in the parameters of the polynomial, in preparation for eventual generalization to a "fit" least squares a curve for a polynomial of degree p.
Proceeding in exactly the same way as we did with the line of least squares, we can apply the difference between each actual value of Y = Y
i
quadratic equation using least squares, which gives us the "distance" vertical D i that alienates both values: D 1 = a 0 + a 1 X 1 + to 2
X
1
Σ
Adjust, as appropriate, a line or a parabola least squares the data given by the following table: The first step required before attempting to set a set of data, a formula is to put the data on a chart to try to discover the trend shown by the data. In this case, the graph is be:
Although at first sight our first impulse is to try to carry out a fit using a least squares line, the dot on the chart to X
0
= 0 if it really is not a mistake in making a reading but a genuinely valid data should lead us to think about the possibility of data rather than being shaped by a straight line may be modeled by a curve. And the curve simplest of all is provided by a second degree polynomial, a quadratic polynomial. Using the normal equations derived above, the least-squares parabola turns out to be: 
Y = 2.51 - 1.20X + 0.733 X ²
The plotting of this curve, superimposed on experimental data, appears as follows:
We can see that the adjustment data to a quadratic formula is pretty good. Not only that, but we can detect the presence of what appears to be a minimum. This minimum could well be an optimal point to minimize losses in an industrial process to obtain the highest degree of purity in a chemical process, or achieve the highest quality alloy. And we use the seven pairs of experimental data to carry out modeling without having to resort to a polynomial of degree six if we insisted on an exact adjustment of the data. We can immediately see the graph that the minimum point of the parable is located approximately at the point X = 0.25, and we can get a better numerical approximation by taking the derivative calculus of the parable of least squares and equating to zero the derivative. Armed with this information, we can plan the conduct of a single experiment in which we give to the variable X
(which presumably is under our control) the value 0.25 in order to confirm whether there really is a point minimum. Note the bold step we are taking here. In a series of discrete points, after carrying out the adjustment of the data to a formula we are anticipating the existence of a minimum, and not only this but we are anticipating the area which is located the lowest. This is precisely one of the goals set a series of data to a formula, you can use this formula to try to make predictions within the range studied, or even extrapolate the formula outside the ranges studied.
PROBLEM:
To determine the value of the constant g, the acceleration due to gravity on Earth's surface, a group of students conducted an experiment which measured the time it took for an object falling from a building along different heights, measuring distances preset time. If the results were as follows:
Considering
t as the independent variable and
and
as the dependent variable, what is the best fit parabola these data? Knowing that the theoretical formula is y = ½ gt ²
from these experimental data. Also calculate the heights, as the curve of least squares, should students have obtained for each of the elapsed times. The plotting of the points obtained experimentally as follows: The graph shows that, within the error margins can be expected in any experiment is performed, data seem to better fit a parabolic curve to a straight line. Using the normal equations derived above, the least-squares parabola turns out to be: Y = 5.089t 2
The continuous plot of this formula superimposed on experimental data which was obtained as follows:
If the formula theoretical acceleration due to gravity on Earth is
y = ½ gt ²
, then the value of such acceleration
g
g
= 10,178 g = 9.8 m / s ²
. The problem shows that a least-squares fit is charged with "average" trend with respect to the experimental data, and the more experimental data are taken, the better. This problem is representative of those problems which previously has been derived and a theoretical model to explain certain behavior of some natural phenomenon, in which the purpose of carrying out a set of data to a formula is to obtain a value for some constant as it is in this case the acceleration of gravity on Earth's surface. http://www.amstat.org/publications/jse/v3n1/datasets.dickey.html
Get the parable of least squares in the form
D = a 0 + to 1
V +
describing the dataset. Based on this formula, estimate the distance D
Based on this formula, the braking distance when the car is moving at 45 mph and 80 mph are:
Note that in this problem to calculate the stopping distance for a
D
Y = a + a 0 1 X + a 2
X ²
+
to 3
X
using what will be the least-squares cubic equation, which gives us the "distance" vertical D i that alienates both values: D 1 = a 0 + a 1 X 1 + to 2
X
1
to 3 , which eventually lead us to four sets of simultaneous equations. Solving these equations simultaneously be exactly the same way as the way in which cases were resolved for the linear regression equation and the parable of least squares, and will not be repeated here. The end result of all this is, as I should have suspected, a set of normal equations for cubic polynomial : to 0 N + a 1 Σ X + a
2
1 X 2
and ignoring the possibility of interaction terms is as follows: Y = α + ß 1 X 1 + ß 2 X 2 + ß
11
1
2 - 0.2 X
force a straight line on this data collection carried out regression analysis, by blindly usual mathematical calculations to obtain the "best fit" linear. However, the formula thus obtained we may not be very useful to estimate what will happen with other values \u200b\u200bare not plotted.
If we get the idea that this data collection can be best described by a non-linear model bx + cx 2 + dx
3
+ ex
4 + ... 
first thing that could happen would we use a polynomial whose degree corresponds directly to the number of dots on the graph. In this way, as well as a graph in which there are only two points we would use a straight line to connect these points on a graph in which there are three points we would use a quadratic polynomial of degree 2, in a game in which there are four points would use a cubic polynomial of degree 3, and so on. This mathematical procedure is known as interpolation
first thing that could happen would we use a polynomial whose degree corresponds directly to the number of dots on the graph. In this way, as well as a graph in which there are only two points we would use a straight line to connect these points on a graph in which there are three points we would use a quadratic polynomial of degree 2, in a game in which there are four points would use a cubic polynomial of degree 3, and so on. This mathematical procedure is known as interpolation
. This certainly would go exactly curve for each points of the graph, as shown below:
Let's look at two examples.
PROBLEM:
For an experiment of which are available only three data shown in the chart below: PROBLEM:
What is the empirical formula can best fit these data? Try perform a least-squares fit to obtain the regression line that best approximates the three data shown in the graph will una pérdida de tiempo, ya que los puntos no muestran tendencia alguna de agruparse en las proximidades de una línea recta. Sin embargo, podemos tratar de llevar a cabo aquí un ajuste utilizando como modelo un polinomio cuadrático, haciendo pasar los tres puntos
exactamente
a lo largo del polinomio:
P(X) = a 0 + a
1
X + a
2 X 
2
2 Sustituyendo los tres pares de datos
A
( X
1
,
Y 1 )=(1,1), B ( X 2
,
Y ,
2 )=(2,8) and C ( X 2 , And 2) = (3,2) in the quadratic polynomial: 1 = a 0 + a 1 (1) + a 2 (1) 2 8 = a 0 + a 1 (2) + a 2 (2) 2
2 = a 0 + a 1 (3 ) + a 2 (3) 2
obtain the following set of equations can be solved as simultaneous equations: to 0 1 + a + a 2
= 1 to + 2a 0 1 to 2 +4 = 8
to the 3rd obtain the following set of equations can be solved as simultaneous equations: to 0 1 + a + a 2
= 1 to + 2a 0 1 to 2 +4 = 8
0
+
1
the 9th + 2 = 2 Of these three equations we obtain as a solution the following factors:
to 0 = -19 to 1 = 26.5
to 2 = -5.5 The quadratic formula to accurately model the three pairs of data is then:
P (X) = - 19 + 26.5X - 6.5X 2 to 0 = -19 to 1 = 26.5
to 2 = -5.5 The quadratic formula to accurately model the three pairs of data is then:
The graph of this quadratic formula superimposed on the three discrete points that produced it is:
If the data were quadratic formula
forced on the data was collected from real life, the difficulty with the method of setting exact If the data were quadratic formula
is that if you subsequently collect additional data values And at other points of X such as X = 1.5 and X = 2.5, such additional points can not be used to refine the model, since its derivation does not support more than three pairs, in which case the gathering of additional data only serve to confirm or reject the quadratic formula obtained, not to improve and refine it.
PROBLEM:
of the following
X = -1, 1 And = 0
X 2 = 0, And
2 = 0
X 3 = 1, 3 And
= 0.1 X 4 = 1.3, And 4
= 1 a cubic polynomial: P (X) = a + a 0
1 X + a 2 + X 2 to 3 X 3
1 X + a 2 + X 2 to 3 X 3
there much data as i coefficients in the polynomial, which allows us to perform accurate adjustment
otherwise could not be carried out if there were fewer data or more data coefficients coefficients. To perform accurate adjustment
simply replace the pairs of values \u200b\u200bfor the cubic polynomial and four equations can be solved as simultaneous linear equations: to 0 + a 1 (-1) + a 2 (-1) 2 + to 3
(-1) = 0 3 to 0 + a 1
(0) + a 2
(0) 2 + to 3 (0) 3 = 0 to 0 + a 1 (1) + a 2
(1) 2 + to 3 (1) 3 = 0.1 to 0 + a 1 (1.3) + a 2
(1.3) 2 + to 3 (1.3) 3 = 1 Of these four equations we obtain the following coefficients: to
0
= 0 to 1 = -0,898 to 2 = 0.05 to 3 = 0,948
The
(1) 2 + to 3 (1) 3 = 0.1 to 0 + a 1 (1.3) + a 2
(1.3) 2 + to 3 (1.3) 3 = 1 Of these four equations we obtain the following coefficients: to
0
= 0 to 1 = -0,898 to 2 = 0.05 to 3 = 0,948
The
cubic polynomial representing the four pairs of data is then:
P (X) = -. 898X + 0.05X + 0.948X 2 3
The cubic polynomial graph superimposed on the four discrete produced it is:
The cubic polynomial graph superimposed on the four discrete produced it is:
All the points fall exactly on the curve
as we had anticipated.
An inspection of the curve shows that three of the points appear to be clustered around what appears to be a line almost horizontal. The only discordant note gives a point on X 4 = 1.3, which should make us reflect.
If the four points provided to make an exact fit to a cubic polynomial have been obtained experimentally, the fact that three of the four points seem to be located around a straight line should make us ask ourselves: there is no possibility of the fourth point is not near that line has been the result of some serious experimental error rather than an error of a statistical nature? Either way, it is necessary to keep an open mind to the possibility that the data point is a genuine discordant, so that if we repeat the experiment only for that point would return to get a result close to that obtained previously. As an alternative to solve this mystery, we can obtain more information by obtaining experimental data for other points that had not been considered, for example X =- 0.5, and X
= +0.5. But in that case is no longer possible to try to carry out an exact fit to a cubic formula, would require in any case a fifth degree polynomial. And if eleven collect experimental data, we would require a polynomial of tenth grade to carry out an exact fit, running the curve on all ten points. Regardless of the mathematical complexity of driving polynomials of increasing order, is the fact that we are giving much importance to force we are modeling the curve to pass exactly 
on all points, which flatly ignores the fact that experimental data always have some measure of statistical "noise, a dose of random error that prevents them from falling on a precise way curve if there is a curve derived theoretically able to describe what we see. On the other hand, the disadvantage of high degree polynomials is their tendency to oscillate violently, not only outside the range of values \u200b\u200bconsidered in an experiment, but even among the points buffer zones in which they carried out the measurements. Note on the curve of third degree polynomial for values \u200b\u200bbelow 1.5 X =-
vertical value falls sharply, going something similar to values \u200b\u200babove
X 
on all points, which flatly ignores the fact that experimental data always have some measure of statistical "noise, a dose of random error that prevents them from falling on a precise way curve if there is a curve derived theoretically able to describe what we see. On the other hand, the disadvantage of high degree polynomials is their tendency to oscillate violently, not only outside the range of values \u200b\u200bconsidered in an experiment, but even among the points buffer zones in which they carried out the measurements. Note on the curve of third degree polynomial for values \u200b\u200bbelow 1.5 X =- vertical value falls sharply, going something similar to values \u200b\u200babove
= +1.5 X where the values \u200b\u200bof P (X) amount sharply. For polynomials of high degree, this oscillatory behavior can turn violent in a matter completely unpredictable, to be a direct consequence of insisting on carrying out an exact modeling then go all the experimental data on a curve.
The interpolation procedure is appropriate to solve problems analytically accurate, which does not happen with the experimental data where the data rarely "fall" just a value that could be considered ideal, where the dispersion of data with respect to a set "ideal" is due to experimental error and where it is meaningless to try to fit exactly a certain amount of data to a polynomial formula. That is why, as well as fitting a linear formula to a collection of data that seem to follow a linear trend to use the method of least squares, the same method of least squares is extended to formulas can be applied to polynomial, allowing us to maintain the degree of the polynomial under control without allowing it to grow disproportionately to be adding additional pairs of points (in other words, under the criterion of least squares we try to fit 101 pairs of points a quadratic polynomial or a cubic polynomial instead of being forced to have recourse to a polynomial of degree 100 if you insist on trying to carry out an exact adjustment data to the formula that we are developing). If a set of data pairs to be plotted does not show a clustering around a straight line but around a curve, as a first approximation we can try to make an "adjustment" to the basic curve of all, the parable
, which in simple terms means attempting to carry out the data fit a quadratic polynomial as follows: Y = a + 0 to 1 X + a
2 X ²
has done a slight change of notation in the parameters of the polynomial, in preparation for eventual generalization to a "fit" least squares a curve for a polynomial of degree p.
Proceeding in exactly the same way as we did with the line of least squares, we can apply the difference between each actual value of Y = Y
1 , Y 2, and 3 And ,..., N
and each value calculated for the corresponding X
and each value calculated for the corresponding X
i
quadratic equation using least squares, which gives us the "distance" vertical D i that alienates both values: D 1 = a 0 + a 1 X 1 + to 2
X 1 ² - Y 1 D 2 = a 0 + a 1 X 2 + to 2
X 2 ² - Y 2 D 3 = a 0 + a 1 X 3
+ a 2 X
3 ² - Y 3 . . . D N = a 0 + a
1
X N
+ a 2 X
² N - Y N And like as we did to find the line least squares, also here we extend the approach of seeking the quadratic polynomial is such that the sum of the squares of the vertical distances of each one of the "real" points calculated according to the polynomial to be a minimum. In short, we want to minimize the function: S = [a 0 + a 1 X 1 + to 2
X 2 ² - Y 2 D 3 = a 0 + a 1 X 3
+ a 2 X
3 ² - Y 3 . . . D N = a 0 + a
1
X N
+ a 2 X
² N - Y N And like as we did to find the line least squares, also here we extend the approach of seeking the quadratic polynomial is such that the sum of the squares of the vertical distances of each one of the "real" points calculated according to the polynomial to be a minimum. In short, we want to minimize the function: S = [a 0 + a 1 X 1 + to 2
X
1
² - And 1 ] ² + [a 0 + a 1 X 2 + a 2 X 2 ² - Y 2] ² + [a 0 + a 1 X 3 + a 2 X 3 ² - Y 3] _______ + ... + [A 0 + a 1 X N + a 2 X
² N - Y N ] ² Since we now we have three parameters instead of two, we must carry out three partial differentiation, which eventually lead us to the following three sets of equations: to 0 N + a 1 Σ X + a 2 Σ
X ² = Σ And to 0 Σ X + a 1 Σ X ² + a
2 Σ
X 3 = Σ XY to 0 Σ X ² + a 1 Σ X
3 + to 2 Σ X 3 = Σ X ² Y This set of equations is known as normal equations to the parable of least squares. Again, we have a system of simultaneous equations with three unknowns, the parameters to 0 , to 1 and to 2 which will define the least squares curve for a given set of data that seem to follow an exponential growth in the second degree.
PROBLEM: 2 Σ
X 3 = Σ XY to 0 Σ X ² + a 1 Σ X
3 + to 2 Σ X 3 = Σ X ² Y This set of equations is known as normal equations to the parable of least squares. Again, we have a system of simultaneous equations with three unknowns, the parameters to 0 , to 1 and to 2 which will define the least squares curve for a given set of data that seem to follow an exponential growth in the second degree.
Adjust, as appropriate, a line or a parabola least squares the data given by the following table: The first step required before attempting to set a set of data, a formula is to put the data on a chart to try to discover the trend shown by the data. In this case, the graph is be:
Although at first sight our first impulse is to try to carry out a fit using a least squares line, the dot on the chart to X
0
= 0 if it really is not a mistake in making a reading but a genuinely valid data should lead us to think about the possibility of data rather than being shaped by a straight line may be modeled by a curve. And the curve simplest of all is provided by a second degree polynomial, a quadratic polynomial. Using the normal equations derived above, the least-squares parabola turns out to be:
Y = 2.51 - 1.20X + 0.733 X ² The plotting of this curve, superimposed on experimental data, appears as follows:
We can see that the adjustment data to a quadratic formula is pretty good. Not only that, but we can detect the presence of what appears to be a minimum. This minimum could well be an optimal point to minimize losses in an industrial process to obtain the highest degree of purity in a chemical process, or achieve the highest quality alloy. And we use the seven pairs of experimental data to carry out modeling without having to resort to a polynomial of degree six if we insisted on an exact adjustment of the data. We can immediately see the graph that the minimum point of the parable is located approximately at the point X = 0.25, and we can get a better numerical approximation by taking the derivative calculus of the parable of least squares and equating to zero the derivative. Armed with this information, we can plan the conduct of a single experiment in which we give to the variable X
(which presumably is under our control) the value 0.25 in order to confirm whether there really is a point minimum. Note the bold step we are taking here. In a series of discrete points, after carrying out the adjustment of the data to a formula we are anticipating the existence of a minimum, and not only this but we are anticipating the area which is located the lowest. This is precisely one of the goals set a series of data to a formula, you can use this formula to try to make predictions within the range studied, or even extrapolate the formula outside the ranges studied.
PROBLEM:
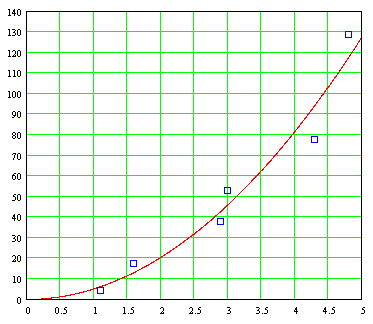
To determine the value of the constant g, the acceleration due to gravity on Earth's surface, a group of students conducted an experiment which measured the time it took for an object falling from a building along different heights, measuring distances preset time. If the results were as follows:
Considering
t as the independent variable and
and
as the dependent variable, what is the best fit parabola these data? Knowing that the theoretical formula is y = ½ gt ²
where g is the acceleration 
of gravity, get the value of g
of gravity, get the value of g from these experimental data. Also calculate the heights, as the curve of least squares, should students have obtained for each of the elapsed times. The plotting of the points obtained experimentally as follows: The graph shows that, within the error margins can be expected in any experiment is performed, data seem to better fit a parabolic curve to a straight line. Using the normal equations derived above, the least-squares parabola turns out to be: Y = 5.089t 2
The continuous plot of this formula superimposed on experimental data which was obtained as follows:
y = ½ gt ²
, then the value of such acceleration
g
be: ½ g
= 5,089
= 5,089
g
= 10,178 g = 9.8 m / s ²
This value compares favorably with the known value of . The problem shows that a least-squares fit is charged with "average" trend with respect to the experimental data, and the more experimental data are taken, the better. This problem is representative of those problems which previously has been derived and a theoretical model to explain certain behavior of some natural phenomenon, in which the purpose of carrying out a set of data to a formula is to obtain a value for some constant as it is in this case the acceleration of gravity on Earth's surface. http://www.amstat.org/publications/jse/v3n1/datasets.dickey.html
PROBLEM:
In investigating automobile accidents, the total time required for the total braking of a car after the driver has received a threat is composed of
reaction time (the time lag in detection of danger the application of the brakes) plus the braking time (the time it takes the car to stop after applying the brakes). The following table provides the stopping distance D in feet of a car traveling at different speeds V in miles per hour at which the driver detects a hazard.
In investigating automobile accidents, the total time required for the total braking of a car after the driver has received a threat is composed of
reaction time (the time lag in detection of danger the application of the brakes) plus the braking time (the time it takes the car to stop after applying the brakes). The following table provides the stopping distance D in feet of a car traveling at different speeds V in miles per hour at which the driver detects a hazard.
Get the parable of least squares in the form
D = a 0 + to 1
V +
2 
V ²
V ² describing the dataset. Based on this formula, estimate the distance D
braking when the car is moving at 45 mph and 80 mph. The least-squares parabola is found to be: D = 41.77 - 1.096V + V ² 08,786 The graph of this formula superimposed on the data given is as follows:
Based on this formula, the braking distance when the car is moving at 45 mph and 80 mph are:
D = 41.77 - 1096 (45) + 08 786 (45) ²
D = 170 feet D = 41.77 - 1,096 (80) + .08786 (80) ² 
D = 516 feet
D = 516 feet
Note that in this problem to calculate the stopping distance for a
D
V speed = 80 mph are
extrapolating data going beyond the speed
V = 70 miles / hour for which were obtained by making a prediction that goes beyond what we might call our "comfort zone." There is always a risk when making such extrapolations, and more than a statistic has been in the ridiculous to make such extrapolations, although in this case the fit of the data to a quadratic formula should give us some reassurance that the actual outcome will not be far from what we predicted.
This problem is representative of those problems in which the conclusions can be drawn from them can have an impact even legal.
The procedure we have studied in this section can be extended to carry out an adjustment of a set of data to a third-degree polynomial, a cubic polynomial
general whose representation is:
extrapolating data going beyond the speed
V = 70 miles / hour for which were obtained by making a prediction that goes beyond what we might call our "comfort zone." There is always a risk when making such extrapolations, and more than a statistic has been in the ridiculous to make such extrapolations, although in this case the fit of the data to a quadratic formula should give us some reassurance that the actual outcome will not be far from what we predicted.
This problem is representative of those problems in which the conclusions can be drawn from them can have an impact even legal.
The procedure we have studied in this section can be extended to carry out an adjustment of a set of data to a third-degree polynomial, a cubic polynomial
general whose representation is:
Y = a + a 0 1 X + a 2
X ²
+
to 3
X
3 now proceed in the same way as we did with the parable of least squares, postulating the difference between each actual value of Y = Y 1 , Y 2, and 3 And ,..., N and each value calculated for the corresponding X
i using what will be the least-squares cubic equation, which gives us the "distance" vertical D i that alienates both values: D 1 = a 0 + a 1 X 1 + to 2
X 1 ² + to X 3 1 3 - Y 1 D 2 = a 0 + a 1 X 2 + a
2
X 2 ² + a 3 X 2 3 - Y 2 D 3 = a 0 + a 1 X 3 + a
2
X 3 ² + a 3 X 3 3 - Y 3 . . . D 1 = a 0 + a
1
X N
+ a 2 X
N ² + to 3 X N 3 - Y 1 And like as we did to find the line of least squares, also here we extend the approach to find the quadratic polynomial is such that the sum of the squares of the vertical distances of each one of the "real" points calculated according to the polynomial is a minimum. In short, we want to minimize the function: S = [a 0 + a 1 X 1 + to 2
2
X 2 ² + a 3 X 2 3 - Y 2 D 3 = a 0 + a 1 X 3 + a
2
X 3 ² + a 3 X 3 3 - Y 3 . . . D 1 = a 0 + a
1
X N
+ a 2 X
N ² + to 3 X N 3 - Y 1 And like as we did to find the line of least squares, also here we extend the approach to find the quadratic polynomial is such that the sum of the squares of the vertical distances of each one of the "real" points calculated according to the polynomial is a minimum. In short, we want to minimize the function: S = [a 0 + a 1 X 1 + to 2
X
1
² + to X 3 1 3 - Y 1 ]² + [a 0 + a 1 X 2 + a 2 X 2 ² + a 3 X 2 3 - Y 2 ]² + [a 0 + a 1 X 3 + a 2 X 3
² + a 3 X 3 3 - Y 3] + ... + [A 0 + a 1 X N + a 2 X N ² + to 3 X N 3 - Y N] ² Now we four parameters instead of three, which means we have to perform some differentiation four with respect to 0 , to 1 , to 2
and
² + a 3 X 3 3 - Y 3] + ... + [A 0 + a 1 X N + a 2 X N ² + to 3 X N 3 - Y N] ² Now we four parameters instead of three, which means we have to perform some differentiation four with respect to 0 , to 1 , to 2
and
to 3 , which eventually lead us to four sets of simultaneous equations. Solving these equations simultaneously be exactly the same way as the way in which cases were resolved for the linear regression equation and the parable of least squares, and will not be repeated here. The end result of all this is, as I should have suspected, a set of normal equations for cubic polynomial : to 0 N + a 1 Σ X + a
2
Σ X² + a 3 Σ X 3 = Σ Y a 0 Σ X + a 1
Σ
X² + a 2 Σ X 3 + a 3 Σ X 4 = Σ XY a 0 Σ X² + a 1
Σ
X 3 + a 2 Σ X 4 + a 3 Σ X 5 = Σ X²Y a 0 Σ X 3
+
a 1 Σ X 4 + a 2 Σ X 5 + to 3 Σ X 6 = Σ X 3 And Note that the formation of normal equations for higher degree polynomials is following a definite pattern, and even we can formulate a "rule" for the normal equations for any polynomial of degree n . However, for polynomials of degree greater than 4, this exercise is futile by the excessive amount of repetitive arithmetic calculations would be carried out if we turn directly to the normal equations are expressed as above, this being the reason why we feel the need to develop a little more sophisticated techniques that allow us to solve the normal equations of a shorthand. Like as when the technique for obtaining the least squares line in a single independent variable X was extended to cover a multiple regression in two or more variables 1 X, X 2 , X 3 , etc., Also the parable of least squares can be extended to carry out an adjustment to a formula with two or more variables in linear and quadratic terms. The general multiple regression formula as simple as possible involving linear and quadratic terms, with only two independent variables X
and Σ
X² + a 2 Σ X 3 + a 3 Σ X 4 = Σ XY a 0 Σ X² + a 1
Σ
X 3 + a 2 Σ X 4 + a 3 Σ X 5 = Σ X²Y a 0 Σ X 3
+
a 1 Σ X 4 + a 2 Σ X 5 + to 3 Σ X 6 = Σ X 3 And Note that the formation of normal equations for higher degree polynomials is following a definite pattern, and even we can formulate a "rule" for the normal equations for any polynomial of degree n . However, for polynomials of degree greater than 4, this exercise is futile by the excessive amount of repetitive arithmetic calculations would be carried out if we turn directly to the normal equations are expressed as above, this being the reason why we feel the need to develop a little more sophisticated techniques that allow us to solve the normal equations of a shorthand. Like as when the technique for obtaining the least squares line in a single independent variable X was extended to cover a multiple regression in two or more variables 1 X, X 2 , X 3 , etc., Also the parable of least squares can be extended to carry out an adjustment to a formula with two or more variables in linear and quadratic terms. The general multiple regression formula as simple as possible involving linear and quadratic terms, with only two independent variables X
1 X 2
and ignoring the possibility of interaction terms is as follows: Y = α + ß 1 X 1 + ß 2 X 2 + ß
11
X 1 + ß 2 22 X 2 2 Given the difficulties to visualize the relationships that take place when we're driving or modeling formulas quadratic multiple regressions involving the Department of Mathematics and Statistics at York University in Ontario, Canada, has made available to students and the academic community in which a page can be viewed dynamically (either three-dimensional rotating surfaces corresponding to a multiple regression or by varying parameters such as the interaction terms) using animated GIF files generated with the help of SAS software package developed and sold by the division of Academic Technology Services (ATS) of the University of California at Los Angeles (UCLA). This page can be downloaded from the following address: http://www.math.yorku.ca/SCS/spida/lm/visreg.html This page has taken a graphics file in three dimensions the following formula : And = 20 to 2 X 1 + 2 2 X - 0.2 X
1
2 - 0.2 X
2 2 The file is as follows (the file with animated effects can be obtained using the page from which it was obtained): While data modeling quadratic surfaces can be carried out by solving the set of normal equations produced by the mathematical model that is being considered, the calculations can be cumbersome and even fastidious when made by hand at this level of complexity, which is why it is preferable to another method in which all you have to do is mount a vector or any securities matrix on which can perform calculations in a short series of steps with the help of a computer program to handle vectors and matrices. This is precisely what we see in the next section where we will try on a general matrix method abridging the steps to be carried out for this type of modeling.
Subscribe to:
Post Comments (Atom)
0 comments:
Post a Comment